Trayectoria

Acabamos de ver que gracias a las ecuaciones paramétricas del movimiento podemos hacernos una muy buena idea de cómo es la curva que describe la pelota en su vuelo; simplemente dimos unos pocos valores al tiempo y representamos las posiciones correspondientes. Lógicamente, cuantos más puntos dibujemos más exacta será la representación de la curva. Pues bien, si dibujamos la curva determinada por todos los puntos por los que pasa un móvil en su movimiento obtenemos la trayectoria del movimiento.

Dado que la trayectoria es una curva, en los siguientes apartados veremos primero cómo podemos obtener la gráfica de la trayectoria y, después, cómo podemos obtener la expresión matemática de dicha trayectoria.

Representación gráfica de la trayectoria

Si conocemos las ecuaciones paramétricas \(x=x(t)\), \(y=y(t)\), \(z=z(t)\) de un movimiento, para hallar la gráfica de la trayectoria solo tenemos que dar valores al parámetro \(t\) (el tiempo) para obtener los puntos \((x,y,z)\) en los que se encuentra el objeto en cada instante, y a partir de estos puntos podemos dibujar la trayectoria.

Sin embargo, como te puedes imaginar, no es fácil representar “a mano” la trayectoria de un objeto que se mueve en tres dimensiones. En ocasiones no es fácil generalizar la trayectoria a partir de unas pocas posiciones; además, puede resultar muy tedioso hacer los cálculos y es bastante engorroso representar puntos en tres dimensiones. Pues bien, este es uno de esos casos en los que un lenguaje de programación como Sage acude en nuestra ayuda para hacer el “trabajo sucio” por nosotros.

Este programa dibuja la trayectoria de la bola, cuyas ecuaciones paramétricas son \(x(t)=2t^2\), \(y(t)=10t\), \(z(t)=10+10t-5t^2\), entre los instantes t=0 s y t=3 s. Ejecútalo para ver cómo es la trayectoria de la bola. Puedes cambiar las ecuaciones paramétricas del movimiento y el intervalo de tiempo para ver cómo se modifica la trayectoria de la partícula.

Ecuación de la trayectoria

Hemos visto cómo, conocidas las ecuaciones paramétricas, podemos dibujar la gráfica de la trayectoria que describe un cuerpo en su movimiento. Veamos ahora cómo podemos expresar analíticamente la ecuación de dicha trayectoria.

Para simplificar este estudio de la trayectoria vamos a dejar de lado por un momento nuestra pelota de tenis y vamos a considerar un objeto que se mueve en el plano. Analizaremos tres maneras diferentes de expresar la curva que representa la trayectoria: las ecuaciones paramétricas, la ecuación explícita y la ecuación implícita.

Ecuaciones paramétricas

Las ecuaciones paramétricas de la trayectoria de un cuerpo que se mueve en el plano XY vienen dadas por: \[ \left.\begin{array}{l} x=x(t) \\ y=y(t) \end{array}\right\} \ \] donde \(t\) es un parámetro que toma valores reales. De esta manera, cada punto \((x,y)\) de la trayectoria queda perfectamente determinado por un valor de \(t\).

Ejercicio

Una curva en el plano está definida por las siguientes ecuaciones paramétricas: \[ \left.\begin{array}{l} x=t-1\\ y=2t \end{array}\right\} \ \] ¿De qué curva se trata?

Para hacernos una idea de cómo es la trayectoria vamos a representar la gráfica de la curva. Dando valores al parámetro t se obtienen los siguientes puntos:

\[ \begin{array}{c|c|c} t & x=t-1 & y=2t\\ \hline 0 & -1& 0\\ 1 & 0 & 2\\ 2 & 1 & 4\\ 3 & 2 & 6 \end{array} \]

Al representar estos puntos se ve claramente que la curva que describe el objeto es una recta (sí, has leído bien: en matemáticas una curva puede ser recta).

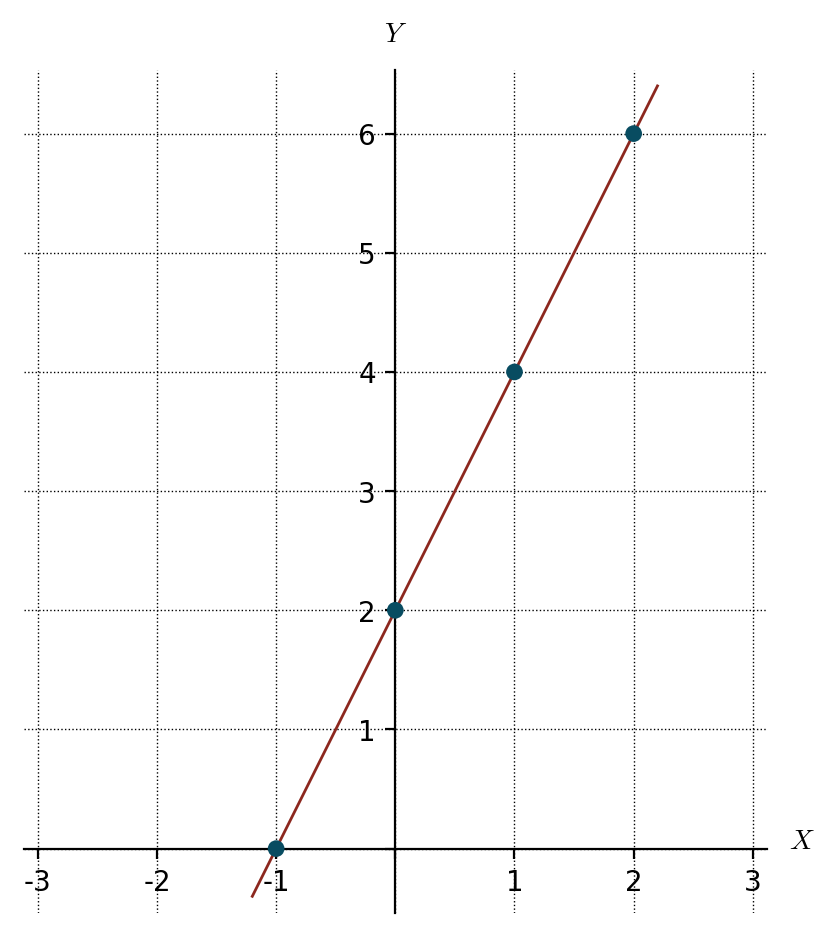
Ecuación explícita

La ecuación explícita de una curva en dos dimensiones es de la forma: \[y=f(x)\] Esta expresión quiere decir que la coordenada \(y\) de cada punto de la trayectoria es una función de la coordenada \(x\). Dicho de otro modo, si conocemos el valor de \(x\) podemos obtener el valor de y sin más que sustituir en la función \(f(x)\).

Es posible obtener la ecuación explícita a partir de las ecuaciones paramétricas. Para ello simplemente debemos “hacer desaparecer” el parámetro \(t\) (el tiempo). ¿Cómo? Despeja la \(t\) de una de las ecuaciones paramétricas y sustituye su valor en la otra ecuación.

Ejercicio

A partir de las ecuaciones paramétricas del ejemplo anterior halla la ecuación de la trayectoria en forma explícita.

Las ecuaciones paramétricas son: \[ \left.\begin{array}{l} x=t-1\\ y=2t \end{array}\right\} \ \] Si despejamos \(t\) en la primera ecuación obtenemos \(t=x+1\). Sustituyendo este valor de \(t\) en la otra ecuación el resultado es \(y=2(x+1)\), es decir: \[y=2x+2\] Esta es la ecuación explícita de la recta que representamos anteriormente.

Ecuación implícita

La ecuación implícita de una curva en el plano es de la forma: \[f(x, y)=0 \] Para obtenerla, en la ecuación implícita pasamos todo a un miembro para que quede una función de las variables \(x\) e \(y\) igualada a cero.

Ejercicio

Halla la ecuación implícita de la trayectoria del ejercicio anterior.

Como la ecuación explícita es \(y=2x+2\), en forma implícita queda:

\[2x-y+2=0\]

Ejemplos de curvas en el plano

A modo de ejemplo mostramos aquí las ecuaciones de unas curvas en el plano que son especialmente importantes, con una explicación del significado geométrico de los parámetros. Algunas ya las conoces, otras las encontrarás más adelante.

Curva	Ecuación	Parámetros	Ejemplo	Descripción
Recta	\[y=mx+n\] \[m, n \in \mathbb{R}\]	\(m\): pendiente de la recta \(n\): ordenada en el origen	\[y=x\]	Recta que pasa por el origen (n=0) y forma un ángulo de 45 grados con el eje X (m=1).
Parábola	\[y=ax^2+bx+c\] \[a, b, c \in \mathbb{R}\] \[a \ne 0\]	\(a>0\): la parábola es “abierta hacia arriba” \(a<0\): la parábola es “abierta hacia abajo”	\[y=x^2\]	Parábola abierta hacia arriba de vértice (0,0).
Circunferencia	\[(x-a)^2+(y-b)^2=r^2\] \[a, b, r \in \mathbb{R}\] \[r >0\]	\((a,b)\): centro de la circunferencia \(r\): radio de la circunferencia	\[x^2+y^2=1\]	Circunferencia de centro (0,0) y radio 1.
Elipse	\[\frac{(x-x_0)^2}{a^2} + \frac{(y-y_0)^2}{b^2}=1\] \[x_0, y_0, a, b \in \mathbb{R}\] \[a>0,b>0,a \ne b\]	\((x_0,y_0)\): coordenadas del centro de la elipse \(a,b\): semiejes	\[\frac{x^2}{4}+\frac{y^2}{1}=1\]	Elipse horizontal centrada en (0,0) de semieje mayor a=2 y semieje menor b=1.

Si quieres ver la representación gráfica de las curvas anteriores, ejecuta este programa:

Para pensar

Volvamos al movimiento en tres dimensiones. Imagina que, en las ecuaciones paramétricas, una de las variables no depende de \(t\). Por ejemplo, si:

\[ \left.\begin{array}{l} x=x(t)\\ y=y(t)\\ z=k \end{array} \right\} \]

con \(k\in \mathbb{R}\), ¿qué podemos saber del movimiento de la partícula?

Ideas clave

➯ La trayectoria es la curva determinada por todos los puntos que ocupa la partícula a lo largo del tiempo.
➯ La ecuación de la trayectoria en el plano se puede expresar, entre otras, en forma paramétrica (\(x(t), y(t), t\in \mathbb{R}\)), explícita (\(y=f(x)\)) e implícita (\(f(x,y)=0\)).