
- 🌓
- Índice
- Vectores
- Objetivos
- Contenidos
- Magnitudes escalares y magnitudes vectoriales
- Vectores
- Elementos de un vector
- Coordenadas de un vector
- Vector nulo
- Vector opuesto
- Vector libre
- Módulo de un vector
- Argumento de un vector
- Test 1
- Suma de vectores
- Producto de un escalar por un vector
- Vector unitario
- Vectores unitarios \(\vec{i}\) y \(\vec{j}\)
- Componentes de un vector
- Test 2
- Vectores en el espacio
- Producto escalar
- Producto vectorial
- Momento de un vector con respecto a un punto
- Test 3
- Ejercicios
- Apéndice: Vectores con Sage
- Movimiento
- Objetivos
- Contenidos
- Lanzamiento de una bola
- Sistema de referencia
- Ecuaciones paramétricas del movimiento
- Trayectoria
- Vector de posición
- Desplazamiento
- Test 1
- Velocidad
- Test 2
- Aceleración
- Componentes intrínsecas de la aceleración
- Clasificación de los movimientos
- Test 3
- Ejercicios
- Lanzamiento en paracaídas
- Fuerzas
- Energía
- Prácticas
- SageMath
Lanzamiento en paracaídas
Problema adaptado del libro Light and Matter de Benjamin Crowell. Los valores de los parámetros han sido tomados del artículo ODE Models for the Parachute Problem de Douglas B. Meade.
“Una paracaidista se lanza desde un avión. ¿Cuál es su velocidad diez segundos después del lanzamiento?”. Probablemente en cursos anteriores tuviste que contestar alguna pregunta de este estilo en más de una ocasión. Para resolver el problema considerarías que, como la paracaidista estaba sometida a una aceleración constante (la famosa aceleración de la gravedad, g), su movimiento era de caída libre y, por tanto, su velocidad se incrementaría de manera constante a medida que iba cayendo. La realidad, sin embargo, es muy diferente. El movimiento de caída de un cuerpo en la Tierra tiene más bien poco de caída libre por un motivo muy simple: la presencia de la atmósfera. Nuestra experiencia diaria nos hace ver que el aire frena la caída de los cuerpos. De hecho, la realidad es que la velocidad de la paracaidista no aumenta de manera constante como sucedería si estuviese cayendo en el vacío de la caída libre, sino que aumenta cada vez en menor proporción. Pues bien, en este ejercicio analizaremos cómo es el movimiento de caída de un paracaidista en presencia de rozamiento con el aire.
Objetivos
Este problema no consiste en sustituir mecánicamente los datos en las ecuaciones y hacer operaciones para obtener una solución. Va a requerir bastante más esfuerzo por tu parte.
- En primer lugar, aplicaremos los conocimientos de cinemática adquiridos a lo largo del tema a la resolución de un problema basado en medidas reales (verás que, por tanto, los cálculos se complican) para obtener los valores de la posición, la velocidad y la aceleración de una persona que se lanza en paracaídas. Pero no nos quedaremos ahí: a la vista de los resultados obtenidos sacaremos conclusiones, veremos cómo el aire afecta a este movimiento comparándolo con el caso ideal de la caída libre, y haremos distintas predicciones con el modelo.
- Al mismo tiempo trabajaremos conceptos matemáticos —estudio y representación gráfica de funciones, cálculo de límites y de derivadas— aplicándolos a un contexto real y analizando su significado físico.
- Así mismo utilizaremos un lenguaje de programación como una herramienta que nos ayude a realizar cálculos que, de otra manera, requerirían bastante tiempo y esfuerzo: representación gráfica de funciones complejas, operaciones repetitivas e, incluso, resolución de ecuaciones que de otro modo serían imposibles de resolver con nuestros conocimientos actuales.
Modelo matemático
Para resolver el problema planteado vamos a recurrir a un modelo matemático, basado en mediciones reales, que predice cómo varía la altura de un paracaidista desde el momento en que salta del avión hasta que abre el paracaídas. Según este modelo su altura \(y\) desde el suelo mientras cae con el paracaídas cerrado viene dada por la siguiente ecuación:
\[ y(t)=b-c \left (t+k\,e^{-\frac tk} \right ) \]donde \(b\), \(c\) y \(k\) son constantes positivas cuyo valor veremos más adelante. En los diversos lanzamientos de prueba analizados para obtener el modelo anterior la apertura del paracaídas se demoró diez segundos desde el momento del lanzamiento; a partir de este instante, debido a la gran superficie del paracaídas desplegado, el aire ejerce una fuerza de frenado mucho mayor, por lo que esta ecuación deja de ser válida.
Consideramos que el movimiento de caída tiene lugar en el eje Y. El cero del sistema de referencia lo tomamos en el suelo, y el instante inicial (t=0 s) es el momento del lanzamiento desde el avión. El dibujo, obviamente, no está a escala. (Imagen: Freepik.es / Beatriz Padín)
Ecuaciones del movimiento
- A partir de la ecuación que nos da el modelo escribe las ecuaciones de la posición, la velocidad y la aceleración en función del tiempo.
- ¿Qué unidades deben tener \(b\), \(c\) y \(k\) para que las ecuaciones sean coherentes?
- Como el movimiento que vamos a analizar es de caída escogemos como sistema de referencia el eje Y y situamos el origen (y=0 m) en el suelo. El instante inicial, t=0 s, lo tomamos en el momento en que la paracaidista salta desde el avión.
Dado que el movimiento es en una dimensión podemos prescindir del carácter vectorial de las magnitudes (ya que todas tienen dirección \(\vec j\)) para trabajar solo con escalares. Sin embargo no podemos olvidar lo siguiente:- Un valor positivo de la posición \(y(t)\) indica que la partícula está situada en la parte positiva del eje Y, mientras que un valor negativo de \(y(t)\) indica que está en la parte negativa del eje (algo que, en este ejercicio, no va a pasar nunca… a menos que la paracaidista caiga en un agujero del suelo).
- Un valor positivo de la velocidad \(v(t)\) quiere decir que el vector velocidad tiene dirección \(+\vec j\) y, por tanto, la paracaidista sube (cosa que tampoco va a suceder); un valor negativo de \(v(t)\) quiere decir que la velocidad tiene dirección \(-\vec j\) y, por tanto, la paracaidista se mueve hacia abajo.
- Si la aceleración \(a(t)\) es positiva el vector aceleración tiene dirección \(+\vec j\), lo cual refleja que la fuerza resultante sobre la paracaidista es vertical y hacia arriba; si \(a(t)\) es negativa entonces el vector aceleración tiene dirección \(-\vec j\) y, por tanto, la fuerza resultante sobre la paracaidista es hacia abajo.
\[ a(t)=-\frac cke^{-\frac tk}\]
- Las unidades de las constantes, en el SI, son: \(b\): metro; \(k\): segundo; \(c\): metro/segundo.
La función que describe la posición en función del tiempo es bastante fácil de derivar. Pero si nos encontramos con otra función más compleja o, simplemente, no nos apetece perder el tiempo haciendo operaciones, SageMath se ocupa de hacerlas por nosotros. Este programa calcula de manera simbólica las derivadas de la posición y la velocidad para obtener, respectivamente, la velocidad y la aceleración de la paracaidista en función del tiempo:
Gráficas del movimiento
La caída mientras el paracaídas está cerrado se puede modelizar con los siguientes valores de los parámetros:
- \(b\) = 1515.4 m
- \(c\) = 53.9 m/s
- \(k\) = 5.5 s
Las funciones que tenemos que representar son:
\[ y(t)=b-c \left (t+k\,e^{-\frac tk} \right ) \] \[ v(t)=-c \left (1-e^{-\frac tk} \right ) \] \[ a(t)=-\frac cke^{-\frac tk}\]
Podemos analizar fácilmente cómo es la función exponencial \(e^{-\frac tk}\); por tanto representar \(a(t)\) y \(v(t)\) no supone un gran problema. Sin embargo, la gráfica de \(y(t)\) requiere un esfuerzo bastante mayor. Tenemos entonces dos opciones: podemos hacer un estudio matemático de las funciones para representarlas o podemos pedirle ayuda a SageMath. En este último caso, las funciones anteriores se pueden representar usando el siguiente programa. Ejecútalo para ver las gráficas.
Las gráficas y-t, v-t y a-t nos dan gran cantidad de información sobre el movimiento. Volveremos a ellas para contestar muchas de las preguntas que se plantean a continuación.
Análisis de la posición
- Halla la altura desde la que cae la paracaidista.
- A los diez segundos del lanzamiento la paracaidista abre el paracaídas. ¿A qué altura se encuentra en este instante?
- Imagina que el movimiento fuese de caída libre, es decir, que no hubiese rozamiento con el aire. En ese caso, al abrirse el paracaídas, ¿la paracaidista estaría más lejos a más cerca del suelo que en el caso con rozamiento? Justifica tu hipótesis y después compruébala numéricamente.
- Dibuja, en los mismos ejes, las gráficas de \(y(t)\) en ambas situaciones —con y sin rozamiento— y compáralas.
La ecuación de la posición \(y(t)=b-c \left (t+k\,e^{-\frac tk} \right )\) nos da la altura a la que se encuentra la paracaidista en cada instante, ya que la coordenada \(y\) está medida desde el suelo.
- \(y(t=0 \;s)=1219 \;m\)
- \(y(t=10 \;s)=928\; m\)
-
El rozamiento del aire frena a la paracaidista en su caída; esto provoca que caiga más despacio que en la caída libre y, por tanto, en los 10 s recorre menos espacio que si no hubiese rozamiento. Por tanto, si el movimiento fuese de caída libre, cuando se abre el paracaídas la paracaidista habría recorrido más espacio y estaría más cerca del suelo (a una menor altura) que en el caso con rozamiento.
Comprobación: escribimos la ecuación de la posición frente al tiempo en el caso de que el movimiento fuese de caída libre y calculamos la altura a la que se encontraría a los 10 s:\[ \left.\begin{array}{l} y_0=1219 \; m\\ v_0=0 \, m/s\\ a=-9.8 \; m/s^2 \end{array}\right\} y(t)=y_0+v_0t+\frac12at^2 \; \Rightarrow y(t)=1219-4,9t^2 \] \[y(t=10 \;s)=729 \;m\]
En caída libre estaría a una altura menor, como habíamos supuesto. -
La gráfica de y-t con rozamiento la hemos obtenido en un apartado anterior. La gráfica y-t en la caída libre se representa a partir de la ecuación del movimiento \(y=1219-4,9t^2\); solo hay que dar unos pocos valores al tiempo, ya que sabemos que se trata de una parábola (o, mejor aún, le pedimos a SageMath que la represente por nosotros).
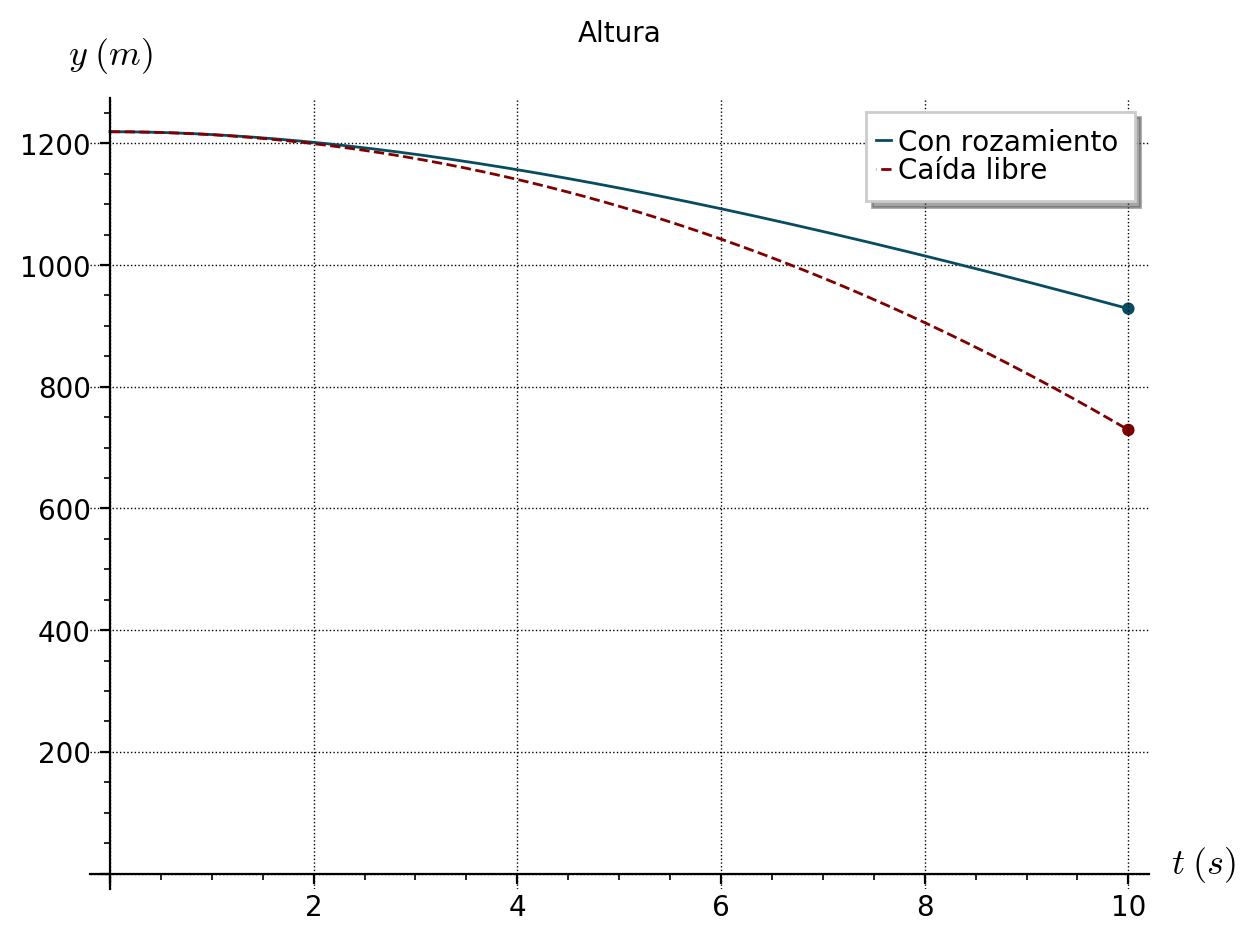
Para un mismo instante la paracaidista estaría más cerca del suelo si cayese en caída libre, ya que no habría rozamiento con el aire que la frenase y por tanto caería a mayor velocidad, recorriendo más espacio.
Análisis de la velocidad
- Halla la velocidad vertical con la que la paracaidista se lanza desde el avión.
- ¿Qué signo tiene la velocidad? Explica su significado.
- A los diez segundos del lanzamiento la paracaidista abre el paracaídas. ¿Qué velocidad lleva este instante?
- Imagina que el movimiento fuese de caída libre, es decir, que no hubiese rozamiento con el aire. En ese caso, al abrirse el paracaídas, ¿la velocidad de la paracaidista sería mayor o menor que en el caso con rozamiento? Justifica tu hipótesis y después compruébala numéricamente.
- Dibuja, en los mismos ejes, las gráficas de \(v(t)\) en ambas situaciones, con y sin rozamiento. Compara ambas gráficas.
A partir de la ecuación \(v(t)=-c \left (1-e^{-\frac tk} \right )\) podemos sacar las siguientes conclusiones:
- \(v(0)=0 \; m/s\), es decir, la paracaidista se deja caer desde el avión.
- Por la gráfica de \(v(t)\) vemos que la velocidad toma solo valores negativos. Esto quiere decir que el movimiento es siempre hacia abajo. El signo de \(v\) también lo podemos justificar, sin necesidad de recurrir a la representación gráfica, a partir de la expresión analítica de \(v(t)\) de la siguiente manera: la función exponencial \(e^{-t/k}\) tiene base mayor que 1 y exponente negativo (ya \(k>0\) y \(t\geqslant 0\)). En consecuencia \(e^{-t/k}\) es siempre menor o igual que 1 y, por tanto,\(1-e^{-t/k}\geqslant 0\); como \(c\) es una constante positiva, el producto \(-c(1-e^{-t/k})\) es siempre negativo.
- \(v(10)=-45,2 \; m/s\)
-
Si el movimiento fuese de caída libre la velocidad sería mayor, porque el aire no la frenaría.
Esta velocidad, en módulo, es mayor que la que nos da el modelo con rozamiento (recuerda que el signo solo indica el sentido del movimiento).
Comprobación: en caída libre la velocidad en función del tiempo es: \[ \left.\begin{array}{l} v_0=0 \, m/s\\ a=-9.8 \; m/s^2 \end{array}\right\} \; v(t)=v_0+at \Rightarrow v(t)=-9,8t \] \[v(t=10 \; s)=-98 \;m/s\] -
Gráficas de \(v(t)\) con y sin rozamiento:
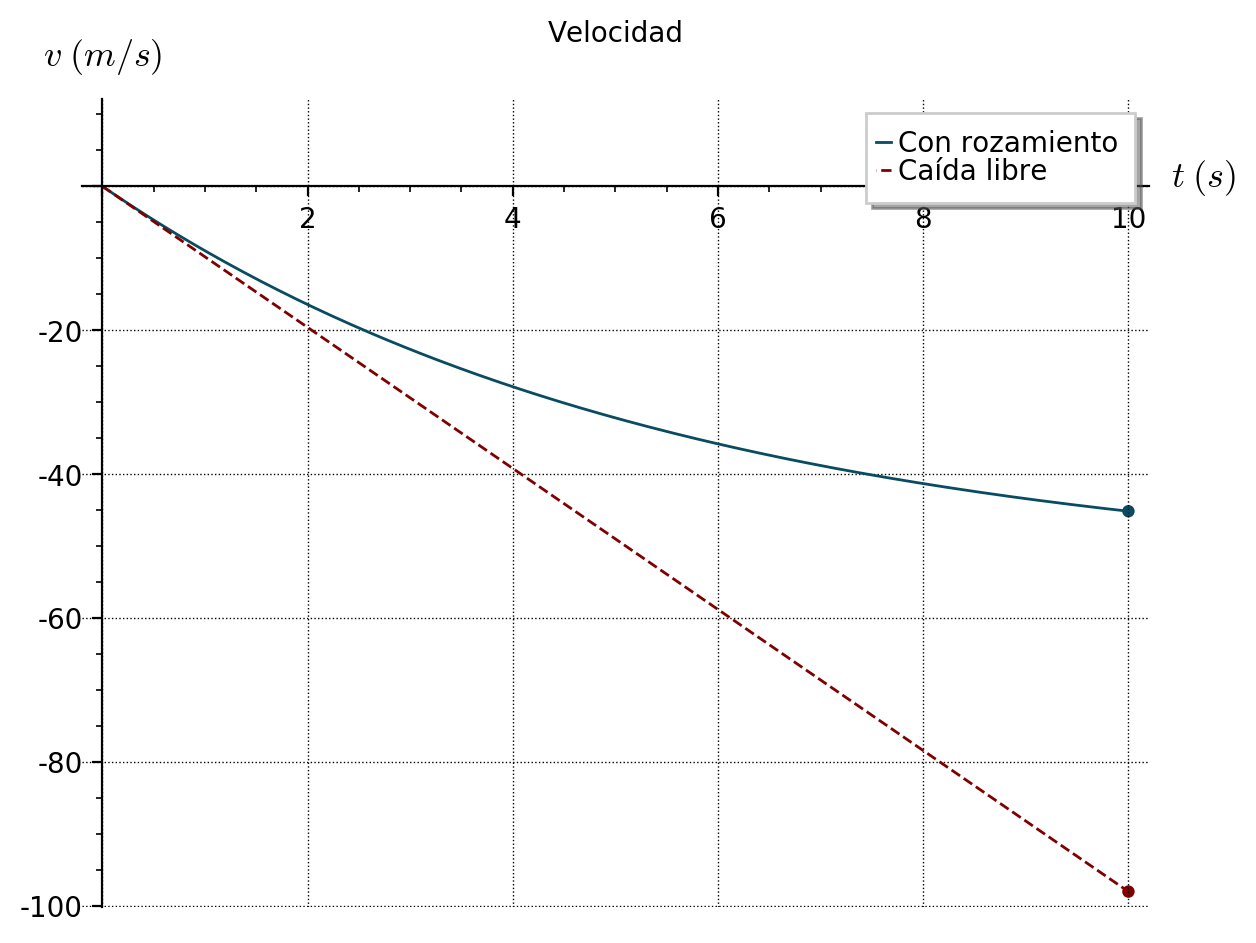
En la caída libre, como el movimiento tiene aceleración constante, la velocidad aumenta de forma proporcional al tiempo, por eso la gráfica es una recta (\(v=-9,8t\)). En el modelo con rozamiento, sin embargo, vemos que la velocidad aumenta más lentamente, ya que la curva se va haciendo cada vez más horizontal. Por eso, según aumenta el tiempo, la velocidad (en módulo) es mayor en el caso de la caída libre que en el caso con rozamiento, como habíamos supuesto previamente.
Análisis de la aceleración
- ¿Qué signo tiene la aceleración? Explica su significado.
- ¿Cómo cambia la aceleración de la paracaidista según va cayendo?
- ¿Cuánto vale la aceleración a los 10 s, en el momento en que la paracaidista abre el paracaídas? ¿Cuánto valdría en este instante si el movimiento fuese de caída libre?
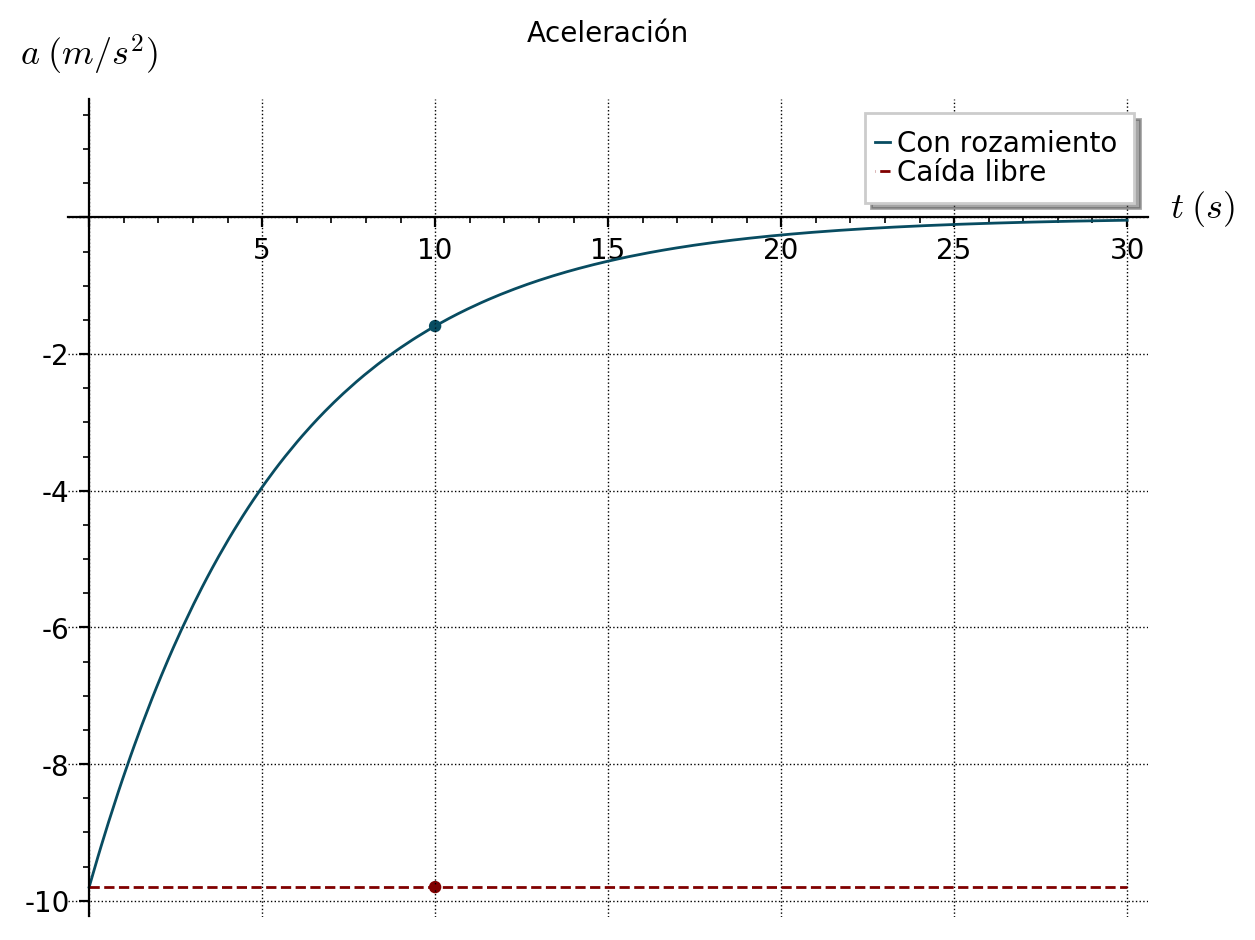
- Dibuja, en los mismos ejes, las gráficas de \(a(t)\) en ambas situaciones (con y sin rozamiento). Compara ambas gráficas.
De la ecuación \(a(t)=-\frac cke^{-\frac tk}\) podemos sacar las siguientes conclusiones:
- La aceleración es negativa, ya que la función exponencial es siempre positiva y \(c\) y \(k\) son constantes positivas. Esto quiere decir que la aceleración experimentada por la paracaidista es hacia abajo, lo cual es consecuencia de una fuerza neta que tira de ella hacia abajo. Además, la velocidad y la aceleración siempre tienen el mismo signo (ambas son negativas), por eso el módulo de la velocidad aumenta (la paracaidista va cada vez más rápido).
- En la gráfica que representamos al principio del ejercicio vemos que, en módulo, la aceleración de caída es cada vez menor. Esto también es fácil de deducir a partir de la expresión analítica de \(a(t)\) ya que, como sabemos, \(e^{-x}\) es una función decreciente y por tanto el módulo de \(a(t)\) decrece (de nuevo recuerda que el signo de a solo nos informa del sentido del vector aceleración).
- \(a(10)=-1,6 \;m/s^2\). En caída libre la aceleración sería \(-9,8 \; m/s^2\), ya que es constante.
-
Gráficas de \(a(t)\) con y sin rozamiento:
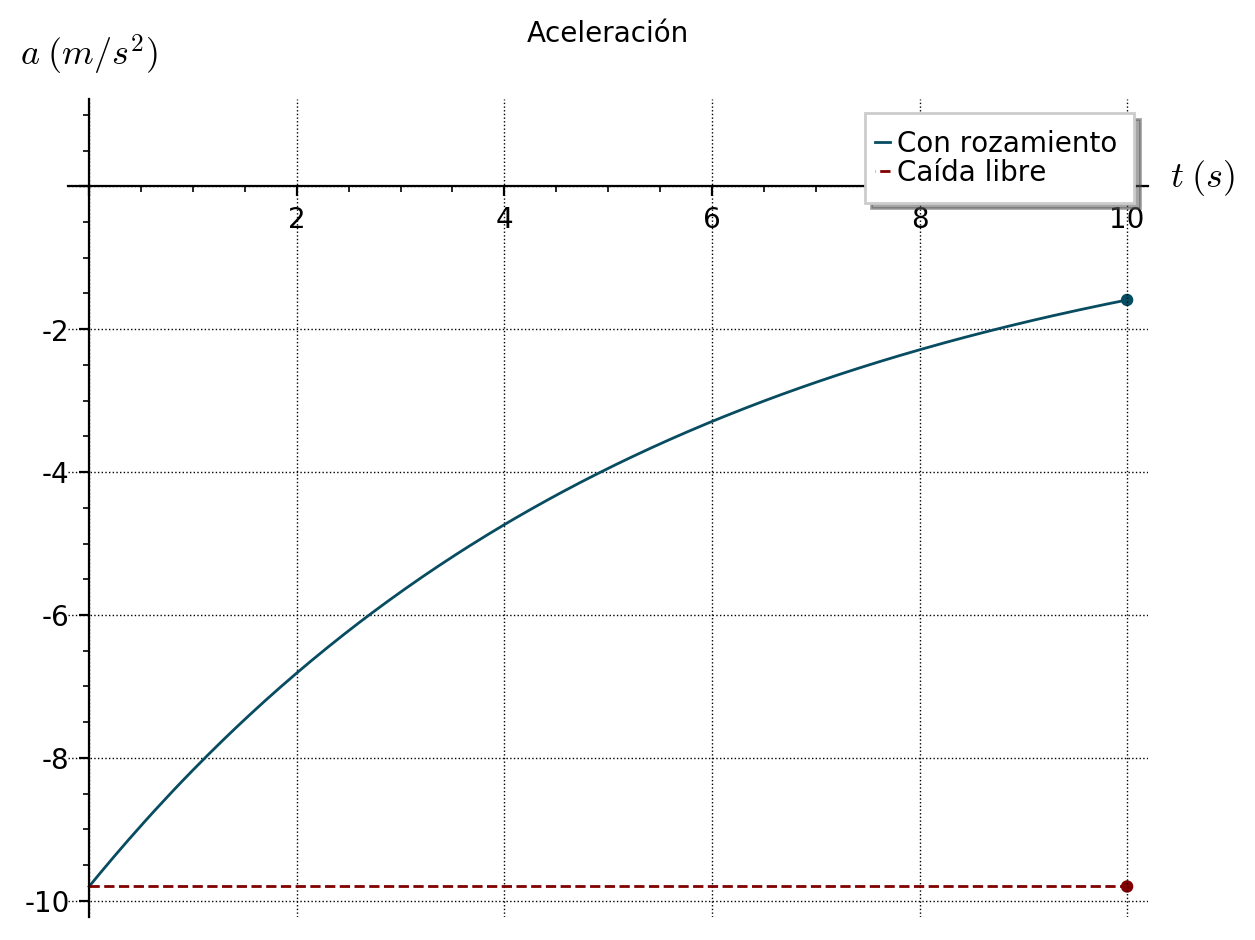
En caída libre la aceleración vale siempre –9,8 m/s2. El rozamiento, sin embargo, hace que esta aceleración sea cada vez más pequeña (en módulo) a medida que la paracaidista va cayendo; este es el motivo por el cual con rozamiento cae “más despacio” que si cayese en el vacío.
Límite cuando \(t\rightarrow \infty\)
En este apartado vamos a ver qué sucedería si, en lugar de abrir el paracaídas a los diez segundos, la paracaidista estuviese cayendo durante un tiempo mucho mayor. De hecho, vamos a analizar el valor que tomarían la velocidad y la aceleración en el caso límite de que el tiempo de caída fuese infinito (lo cual, en Física, quiere decir un tiempo suficientemente largo). Para ello, recuerda que la función exponencial \(e^{−x}\) se aproxima a cero cuando x tiende a más infinito.
- ¿Qué significado físico tiene la constante \(c\)? Una pista: fíjate en la expresión de \(v(t)\) y calcula su límite cuando \(t\rightarrow \infty\).
- Si la paracaidista tarda mucho tiempo en abrir el paracaídas, ¿qué le sucede a su aceleración?
- Compara, para valores grandes de t, las gráficas v-t y a-t en los casos con y sin rozamiento.
- El límite de \(v\) cuando t tiende a infinito es \(-c\): \[\lim_{t\rightarrow \infty}v(t)=\lim_{t\rightarrow \infty}-c \left (1-e^{-\frac tk} \right )=-c\] Este límite quiere decir que en el “mundo real” con rozamiento del aire la velocidad de los objetos que caen desde una altura suficiente tiende a un valor constante, \(c\), al que se le denomina velocidad terminal (en el “mundo ideal” de la caída libre los cuerpos aumentan indefinidamente su velocidad).
-
El límite de \(a\) cuando t tiende a infinito es cero: \[\lim_{t\rightarrow \infty}a(t)=\lim_{t\rightarrow \infty}-\frac cke^{-\frac tk}=0\]
Es decir, si la paracaidista espera lo suficiente para abrir el paracaídas su aceleración será muy pequeña (de ahí que se alcance la velocidad terminal). Veremos en el tema de Dinámica que esto es debido a que llega un momento en que la fuerza de rozamiento del aire, que es contraria al movimiento y depende de la velocidad con que cae el cuerpo, iguala a la fuerza de la gravedad y ambas se anulan, con lo que el cuerpo se mueve sin aceleración. -
Gráficas v-t y a-t:
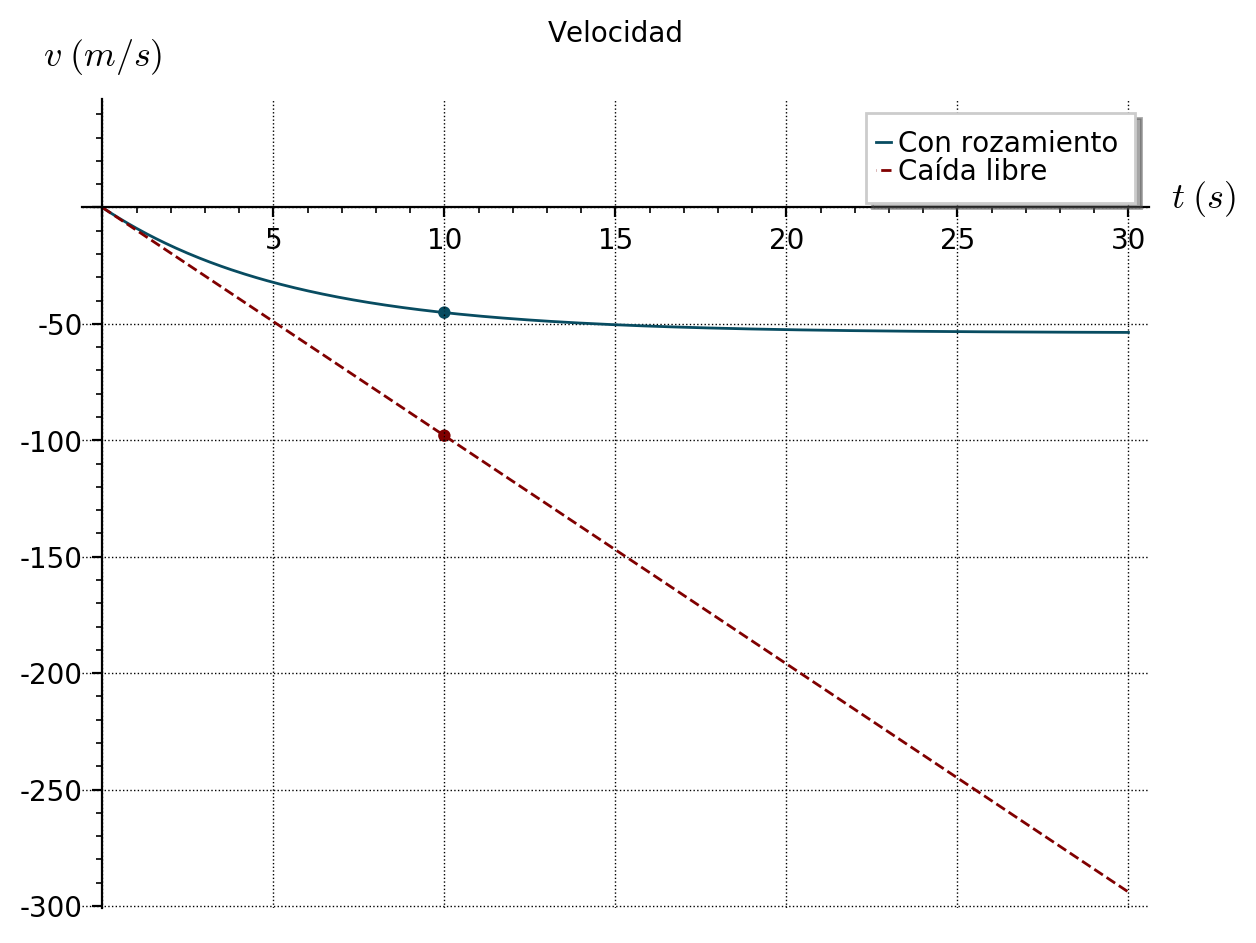
Al comparar ambas gráficas de la velocidad se ve claramente cómo en el caso de rozamiento la velocidad aumenta cada vez menos hasta hacerse prácticamente constante a partir de los 20 s aproximadamente (cuando alcanza la velocidad terminal), mientras en la caída libre la velocidad aumenta sin límite. Según acabamos de calcular, la velocidad terminal es \(-c\), es decir, \(v_{terminal}=-53,9 \; m/s\); fíjate en la gráfica que este valor es la asíntota horizontal cuando \(t\rightarrow +\infty\).
La aceleración en la caída con rozamiento es una función exponencial que tiende a cero cuando t tiende a infinito. En caída libre, sin embargo, la aceleración es constante a lo largo de todo el movimiento.
Otra de las ayudas que ofrece SageMath es el cálculo de límites. Aunque es sencillo realizar estos cálculos a mano, en alguna ocasión nos puede resultar muy ventajoso que alguien los haga por nosotros.
Impacto con el suelo
Imagina que no se abre el paracaídas…
- Utilizando los resultados que obtuvimos anteriormente, si no se abre el paracaídas, ¿cuánto valdrían, aproximadamente, la velocidad y la aceleración de la paracaidista en el impacto con el suelo?
- ¿Puedes calcular cuánto tiempo tardaría en impactar con el suelo?
- Si sigue cayendo sin abrir el paracaídas su velocidad se acercará a la velocidad terminal y su aceleración tenderá a cero.
-
El suelo está en la posición y=0 m. Por tanto para calcular el instante de impacto con el suelo hay que sustituir este valor en la ecuación de \(y(t)\) y despejar el tiempo: \[ \left.\begin{array}{l} y=1515,4-53,9\left (t+5,5\,e^{-\frac {t}{5,5}} \right )\\ y=0 \end{array}\right\} 1515,4-53,9\left (t+5,5\,e^{-\frac {t}{5,5}} \right )=0 \] Llegados a este punto nos encontramos con un problema: no sabemos cómo resolver esta ecuación. Pues bien, este es otro de esos casos en los que la ayuda de SageMath resulta inestimable. Antes de resolver la ecuación, sin embargo, vamos a representar la gráfica y-t para hacernos una idea de cuánto tiempo tardaría la paracaidista en llegar al suelo:
Al ejecutar el programa anterior puedes ver que, según la gráfica posición-tiempo, el tiempo de impacto está alrededor de 28 s. Por tanto buscaremos la solución de la ecuación \(y(t)=0\) en el intervalo [27,29]:
Al ejecutar el programa obtenemos que, si no se abriese el paracaídas, la paracaidista tardaría 28,1 s en impactar contra el suelo.
Con este valor podemos calcular exactamente la velocidad y la aceleración en el momento del impacto sin más que sustituir ese instante en la ecuación correspondiente, y obtenemos los valores:\[ t_{impacto}=28,1 \; s \Rightarrow \left\{\begin{array}{l} v_{impacto}=-53,6 \; m/s\\ a_{impacto}=-0,0594 \; m/s^2 \end{array}\right. \]
Como habíamos supuesto, la velocidad es casi la terminal y la aceleración es prácticamente cero. Los cerca de 200 km/h con los que la paracaidista alcanzaría el suelo no dan mucha opción de supervivencia; la apertura del paracaídas en el momento adecuado habría disminuido esta velocidad terminal hasta dejarla en unos seguros 15-20 km/h.
Investigación
Para finalizar, investiga por tu cuenta sobre los siguientes aspectos:
- ¿De qué factores depende la fuerza de rozamiento del aire?
- ¿Por qué se alcanza la velocidad terminal?
- ¿Cuál es la máxima velocidad a la que puede impactar un paracaidista con el suelo para no sufrir daños?